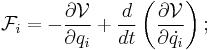Monogenic system

In physics, among the most studied physical systems in classical mechanics are monogenic systems. A monogenic system has excellent mathematical characteristics and is very well suited for mathematical analysis. It is considered a logical starting point for any serious physics endeavour.

In a physical system, if all forces, with the exception of the constraint forces, are derivable from the generalized scalar potential, and this generalized scalar potential is a function of generalized coordinates, generalized velocities, or time, then, this system is a monogenic system.

Expressed using equations, the exact relationship between generalized force 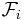$\mathcal{F}_i\,\!$ and generalized potential 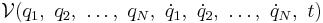$\mathcal{V}(q_1,\ q_2,\ \dots,\ q_N,\ \dot{q}_1,\ \dot{q}_2,\ \dots,\ \dot{q}_N,\ t)\,\!$ is as follows:

$\mathcal{F}_i= - \frac{\partial \mathcal{V}}{\partial q_i}%2B\frac{d}{dt}\left(\frac{\partial \mathcal{V}}{\partial \dot{q_i}}\right);\,$

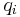where $q_i\,\!$ is generalized coordinate, 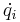$\dot{q_i} \,$ is generalized velocity, and 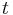$t\,\!$ is time.

If the generalized potential in a monogenic system depends only on generalized coordinates, and not on generalized velocities and time, then, this system is a conservative system.The relationship between generalized force and generalized potential is as follows:

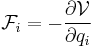$\mathcal{F}_i= - \frac{\partial \mathcal{V}}{\partial q_i}\,$ ；

Lagrangian mechanics often involves monogenic systems. If a physical system is both a holonomic system and a monogenic system, then it’s possible to derive Lagrange's equations from d'Alembert's principle; it's also possible to derive Lagrange's equations from Hamilton's principle^[1].

References

^ Goldstein, Herbert (1980). Classical Mechanics (3rd ed.). United States of America: Addison Wesley. pp. 18–21, 45. ISBN 0201657023.

Monogenic system

See also

References